1.10 Complement of a Set

NCERT Class 11 Mathematics Textbook for blind and visually impaired students made screen readable by Professor T K Bansal.

Let U be the universal set which consists of all prime numbers, and A be the subset of U which consists of all those prime numbers that are not divisors of 42. Thus, A = {x : x ∈ U and x is not a divisor of 42 }.

We see that 2 ∈ U but 2 ∉ A, because 2 is divisor of 42. Similarly, 3 ∈ U but 3 ∉ A, and 7 ∈ U but 7 ∉ A. Now 2, 3 and 7 are the only elements of U which do not belong to Set A. The set of these three prime numbers, i.e., the set {2, 3, 7} is called the Complement of Set A with respect to U, and is denoted by A′. So we have A′ = {2, 3, 7}.

Thus, we see that A′ = {x : x ∈ U and x ∉ A }.

This leads to the following definition.

Definition 8

'Let U be the universal set and A be a subset of U. Then the complement of A is the set of all elements of U which are not the elements of A.'

Symbolically, we write A′ to denote the complement of A with respect to U. Thus,

A′ = {x : x ∈ U and x ∉ A }.

Obviously A′ = U − A

We note that the complement of a set A can be looked upon, alternatively, as the difference between a universal set U and the set A.

Example 20

Let


U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, and


A = {1, 3, 5, 7, 9}.


Find A′.

Solution:

We note that 2, 4, 6, 8, 10 are the only elements of U which do not belong to A.


Hence A′ = { 2, 4, 6, 8,10 }.

Example 21

Let U be universal set of all the students of Class 11 of a coeducational school and


A be the set of all girls in Class 11.


Find A′.

Solution:

Since A is the set of all girls, A′ is clearly the set of all boys in the class.


Note If A is a subset of the universal set U, then its complement A′ is also a subset of U.


Again in Example 20 above, we have A′ = { 2, 4, 6, 8, 10 }

Hence (A′ )′ = {x : x ∈ U and x ∉ A′}


= {1, 3, 5, 7, 9} = A

It is clear from the definition of the complement that for any subset of the universal set U, we have

( A′ )′ = A

Now, we want to find the results for ( A ∪ B ) ′ and A′ ∩ B′ in the following example.

Example 22

Let,


U = {1, 2, 3, 4, 5, 6},


A = {2, 3}, and


B = {3, 4, 5}.


Find A′, B′, A′ ∩ B′, A ∪ B and


hence show that ( A ∪ B ) ′ = A′ ∩ B′.

Solution:

Clearly,


A′ = {1, 4, 5, 6},


B′ = { 1, 2, 6 }.


Hence


A′ ∩ B′ = { 1, 6 }

Also,


A ∪ B = { 2, 3, 4, 5 },


so that


(A ∪ B ) ′ = { 1, 6 }


( A ∪ B ) ′ = { 1, 6 } = A′ ∩ B′

It can be shown that the above result is true in general.


If A and B are any two subsets of the universal set U, then


( A ∪ B ) ′ = A′ ∩ B′.

Similarly,


( A ∩ B ) ′ = A′ ∪ B′ .

These two results are stated in words as follows :

The complement of the union of two sets is the intersection of their complements and


the complement of the intersection of two sets is the union of their complements.


These are called 'De Morgan’s laws'. These are named after the mathematician De Morgan.

The complement A′ of a set A can be represented by a Venn diagram as shown in Figure 1.10.

Figure 1.10

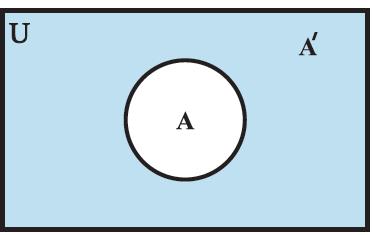
The shaded portion represents the complement of the set A.

Some Properties of Complement Sets

1. Complement laws:


(i) A ∪ A′ = U


(ii) A ∩ A′ = φ

2. De Morgan’s law:


(i) (A ∪ B)′ = A′ ∩ B′


(ii) (A ∩ B ) ′ = A′ ∪ B′

3. Law of double complementation :


(A′ )′ = A

4. Laws of empty set and universal set:


φ′ = U, and U′ = φ.

These laws can be verified by using Venn diagrams.

EXERCISE 1.5

Question 1.


Let, U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 },


A = { 1, 2, 3, 4},


B = { 2, 4, 6, 8 }, and


C = { 3, 4, 5, 6 }.


Find


(i) A′


(ii) B′


(iii) (A ∪ C)′


(iv) (A ∪ B)′


(v) (A′)′


(vi) (B − C)′

Answer 1.


(i) { 5, 6, 7, 8, 9}


(ii) {1, 3, 5, 7, 9 }


(iii) {7, 8, 9 }


(iv) { 5, 7, 9 }


(v) { 1, 2, 3, 4 }


(vi) { 1, 3, 4, 5, 6, 7, 9 }

Question 2.


If U = { a, b, c, d, e, f, g, h},


find the complements of the following sets :


(i) A = {a, b, c}


(ii) B = {d, e, f, g}


(iii) C = {a, c, e, g}


(iv) D = { f, g, h, a}

Answer 2.


(i) { d, e, f, g, h}


(ii) { a, b, c, h }


(iii) { b, d , f, h }


(iv) { b, c, d, e }

Question 3.


Taking the set of natural numbers as the universal set, write down the complements of the following sets:


(i) {x : x is an even natural number}


(ii) { x : x is an odd natural number }


(iii) {x : x is a positive multiple of 3}


(iv) { x : x is a prime number }


(v) {x : x is a natural number divisible by 3 and 5}


(vi) { x : x is a perfect square }


(vii) { x : x is a perfect cube}


(viii) { x : x + 5 = 8 }


(ix) { x : 2x + 5 = 9}


(x) { x : x ≥ 7 }


(xi) { x : x ∈ N and 2x + 1 > 10 }

Answer 3.


(i) { x : x is an odd natural number }


(ii) { x : x is an even natural number }


(iii) { x : x ∈ N and x is not a multiple of 3 }


(iv) { x : x is a positive composite number or x = 1 }


(v) { x : x is a positive integer which is not divisible by 3 or not divisible by 5}


(vi) { x : x ∈ N and x is not a perfect square }


(vii) { x : x ∈ N and x is not a perfect cube }


(viii) { x : x ∈ N and x ≠ 3 }


(ix) { x : x ∈ N and x ≠ 2 }


(x) { x : x ∈ N and x < 7 }


(xi) { x : x ∈ N and x ≤ 9/2}

Question 4.


If


U = {1, 2, 3, 4, 5, 6, 7, 8, 9 },


A = {2, 4, 6, 8}, and


B = { 2, 3, 5, 7}.


Verify that


(i) (A ∪ B)′ = A′ ∩ B′


(ii) (A ∩ B)′ = A′ ∪ B′

Question 5.


Draw appropriate Venn diagram for each of the following :


(i) (A ∪ B) ′,


(ii) A′ ∩ B′,


(iii) (A ∩ B) ′,


(iv) A′ ∪ B′

Question 6.


Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, what is A′?

Answer 6.


A′ is the set of all equilateral triangles.

Question 7.


Fill in the blanks to make each of the following a true statement :


(i) A ∪ A′ = ...


(ii) φ′ ∩ A = ...


(iii) A ∩ A′ = ...

(iv) U′ ∩ A = ...

Answer 7.


(i) U


(ii) A


(iii) φ


(iv) φ