1.9 Operations on Sets

NCERT Class 11 Mathematics Textbook for blind and visually impaired students made screen readable by Professor T K Bansal.

In earlier classes, we have learnt how to perform the operations of addition, subtraction, multiplication and division on numbers. Each one of these operations was performed on a pair of numbers, to get another number. For example, when we perform the operation of addition on the pair of numbers 5 and 13, we get the number 18. Again, performing the operation of multiplication on the pair of numbers 5 and 13, we get 65. Similarly, there are some operations which when performed on two sets give rise to another set. We will now define certain operations on sets and examine their properties. Henceforth, we will refer all our sets as subsets of some universal set.

1.9.1 Union of sets

Let A and B be any two sets. The union of A and B is the set which consists of all the elements of Set A and all the elements of Set B, the common elements being taken only once. The symbol ∪ is used to denote the union. Symbolically, we write A ∪ B and usually read it as ‘A union B’.

Example 12

Let


A = { 2, 4, 6, 8} and


B = { 6, 8, 10, 12}.


Find A ∪ B.

Solution:

We have, A ∪ B = {2, 4, 6, 8, 10, 12}

Note that the common elements 6 and 8 have been taken only once while writing A ∪ B.

Example 13

Let,


A = { a, e, i, o, u } and


B = { a, i, u }.


Show that A ∪ B = A.

Solution:

We have, A ∪ B = { a, e, i, o, u } = A.

This example illustrates that union of sets A and its subset B is the set A itself, i.e., if B ⊂ A, then A ∪ B = A.

Example 14

Let, X = {Ram, Geeta, Akbar}, be the set of students of Class 11, who are in school hockey team.


Let, Y = {Geeta, David, Ashok}, be the set of students from Class 11 who are in the school football team.


Find X ∪ Y and interpret the set.

Solution:

We have, X ∪ Y = {Ram, Geeta, Akbar, David, Ashok}.

This is the set of students from Class 11 who are in the hockey team or in the football team or in both.

Thus, we can define the union of two sets as follows:

Definition 6

'The union of two sets A and B is the set C which consists of all those elements which are either in A or in B (including those which are in both). In symbols, we write.

A ∪ B = { x : x ∈ A or x ∈ B }

The union of two sets can be represented by a Venn diagram as shown in Figure 1.4.

Figure 1.4

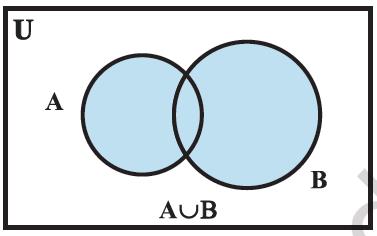
The shaded portion in Fig 1.4 represents A ∪ B.

Some Properties of the Operation of Union

(i) A ∪ B = B ∪ A (Commutative law)


(ii) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C) (Associative law )


(iii) A ∪ φ = A (Law of identity element, φ is the identity of ∪)


(iv) A ∪ A = A (Idempotent law)


(v) U ∪ A = U (Law of U)

1.9.2 Intersection of sets

The intersection of sets A and B is the set of all elements which are common to both Set A and Set B.

The symbol ∩ is used to denote the intersection.

The intersection of two sets A and B is the set of all those elements which belong both to A and B.

Symbolically, we write


A ∩ B = {x : x ∈ A and x ∈ B}.

Example 15

Consider the sets A and B of Example 12. Find A ∩ B.

Solution:

We see that 6, and 8 are the only elements which are common both to A and B. Hence A ∩ B = { 6, 8 }.

Example 16

Consider the sets X and Y of Example 14. Find X ∩ Y.

Solution:

We see that element ‘Geeta’ is the only element common to both.

Hence, X ∩ Y = {Geeta}.

Example 17

Let,


A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, and


B = { 2, 3, 5, 7 }.


Find A ∩ B and hence show that A ∩ B = B.

Solution:

We have A ∩ B = { 2, 3, 5, 7 } = B.

We note that if B ⊂ A; then A ∩ B = B.

Definition 7

'The intersection of two sets A and B is the set of all those elements which belong both to Set A and Set B.'

Symbolically, we write


A ∩ B = {x : x ∈ A and x ∈ B}

The shaded portion in Figure 1.5 indicates the intersection of A and B.

Figure 1.5

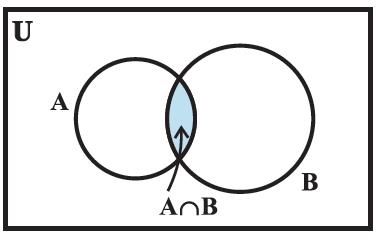
If A and B are two sets such that A ∩ B = φ, then A and B are called disjoint sets.

For example, let


A = { 2, 4, 6, 8 } and


B = { 1, 3, 5, 7 }.


Then A and B are disjoint sets, because there are no elements which are common both to Set A and Set B.

The disjoint sets can be represented by means of Venn diagram as shown in the Figure 1.6 In the above diagram,

A and B are disjoint sets.

Figure 1.6

Some Properties of Operation of Intersection

(i) A ∩ B = B ∩ A (Commutative law).


(ii) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) (Associative law).


(iii) φ ∩ A = φ, and, U ∩ A = A (Law of φ and U).


(iv) A ∩ A = A (Idempotent law)


(v) A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) (Distributive law )


i. e., ∩ distributes over ∪

This can be seen easily from the following Venn diagrams [Figures 1.7 (i) to (v)].

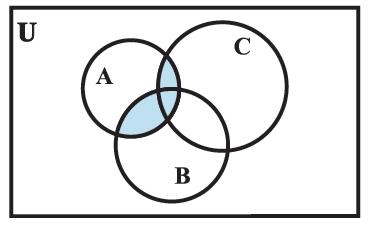
Figure 1.7 (i) (B ∪ C)

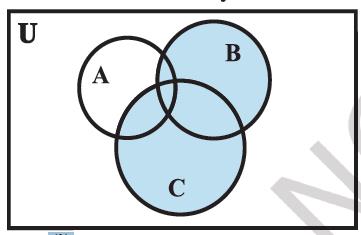
Figure 1.7 (ii) ( A ∩ B )

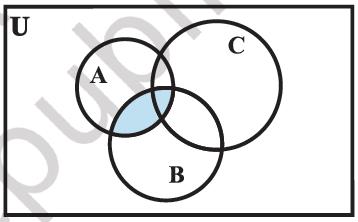
Figure 1.7 (iii) A ∩ ( B ∪ C )

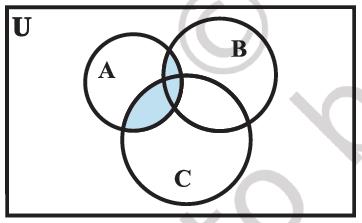
Figure 1.7 (iv) ( A ∩ C )

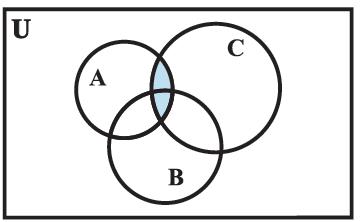
Figure 1.7 (v) ( A ∩ B ) ∪ ( A ∩ C )

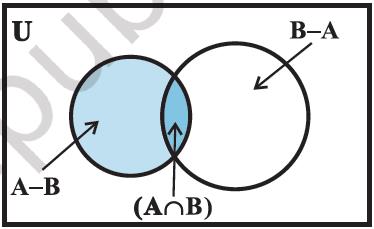
1.9.3 Difference of sets

The difference of two sets A and B in this order is the set of elements which belong to A but not to B.

Symbolically, we write A − B and read as “ A minus B”.

Example 18

Let,


A = { 1, 2, 3, 4, 5, 6},


B = { 2, 4, 6, 8 }.


Find A − B and B − A.

Solution:

We have, A − B = { 1, 3, 5 }, since the elements 1, 3, 5 belong to A but not to B and


B − A = { 8 }, since the element 8 belongs to B and not to A.

We note that A − B ≠ B − A.

Example 19

Let,


V = { a, e, i, o, u } and


B = { a, i, k, u}.


Find V − B and B − V

Solution:

We have,


V − B = { e, o }, since the elements e, o belong to V but not to B and


B − V = { k }, since the element k belongs to B but not to V.

We note that V − B ≠ B − V.

Using the set builder notation, we can rewrite the definition of difference of two sets, as

A − B = { x : x ∈ A and x ∉ B }

The difference of two sets A and B can be represented by Venn diagram as shown in Figure 1.8. The shaded portion represents the difference of the two sets A and B.

Figure 1.8

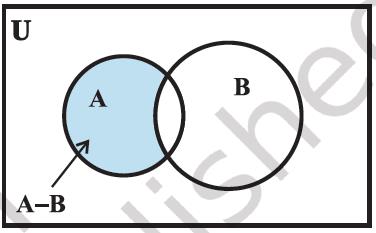
Remark: The sets A − B, A ∩ B and B − A are mutually disjoint sets, i.e., the intersection of any of these two sets is the null set as shown in Figure 1.9.

Figure 1.9

EXERCISE 1.4

Question 1.


Find the union of each of the following pairs of sets :


(i) X = {1, 3, 5}, Y = {1, 2, 3}


(ii) A = [ a, e, i, o, u}, B = {a, b, c}


(iii) A = {x : x is a natural number and multiple of 3}, B = {x : x is a natural number less than 6}


(iv) A = {x : x is a natural number and 1 < x ≤ 6 }, B = {x : x is a natural number and 6 < x < 10 }


(v) A = {1, 2, 3}, B = φ

Answer 1.


(i) X ∪ Y = {1, 2, 3, 5 }


(ii) A ∪ B = { a, b, c, e, i, o, u }


(iii) A ∪ B = {x : x = 1, 2, 4, 5 or a multiple of 3 }


(iv) A ∪ B = {x : 1 < x < 10, x ∈ N}


(v) A ∪ B = {1, 2, 3 }

Question 2.


Let,


A = { a, b },


B = {a, b, c}.


Is A ⊂ B ? What is A ∪ B ?

Answer 2.


Yes, A ∪ B = { a, b, c }

Question 3.


If A and B are two sets such that A ⊂ B, then what is A ∪ B ?

Answer 3.


B

Question 4.


If


A = {1, 2, 3, 4},


B = {3, 4, 5, 6},


C = {5, 6, 7, 8 } and


D = { 7, 8, 9, 10 };


find


(i) A ∪ B


(ii) A ∪ C


(iii) B ∪ C


(iv) B ∪ D


(v) A ∪ B ∪ C


(vi) A ∪ B ∪ D


(vii) B ∪ C ∪ D

Answer 4.


(i) { 1, 2, 3, 4, 5, 6 }


(ii) {1, 2, 3, 4, 5, 6, 7, 8 }


(iii) {3, 4, 5, 6, 7, 8 }


(iv) {3, 4, 5, 6, 7, 8, 9, 10}


(v) {1, 2, 3, 4, 5, 6, 7, 8 }


(vi) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}


(vii) { 3, 4, 5, 6, 7, 8, 9, 10 }

Question 5.


Find the intersection of each pair of sets of question 1 above.

Answer 5.


(i) X ∩ Y = { 1, 3 }


(ii) A ∩ B = { a }


(iii) { 3 }


(iv) φ


(v) φ

Question 6.


If


A = { 3, 5, 7, 9, 11 },


B = {7, 9, 11, 13},


C = {11, 13, 15}and


D = {15, 17};


find


(i) A ∩ B


(ii) B ∩ C


(iii) A ∩ C ∩ D


(iv) A ∩ C


(v) B ∩ D


(vi) A ∩ (B ∪ C)


(vii) A ∩ D


(viii) A ∩ (B ∪ D)


(ix) ( A ∩ B ) ∩ ( B ∪ C )


(x) ( A ∪ D) ∩ ( B ∪ C)

Answer 6.


(i) { 7, 9, 11 }


(ii) { 11, 13 }


(iii) φ


(iv) { 11 }


(v) φ


(vi) { 7, 9, 11 }


(vii) φ


(viii) { 7, 9, 11 }


(ix) {7, 9, 11 }


(x) { 7, 9, 11, 15 }

Question 7.


If


A = {x : x is a natural number },


B = {x : x is an even natural number},


C = {x : x is an odd natural number} and


D = {x : x is a prime number },


find


(i) A ∩ B


(ii) A ∩ C


(iii) A ∩ D


(iv) B ∩ C


(v) B ∩ D


(vi) C ∩ D

Answer 7.


(i) B


(ii) C


(iii) D


(iv) φ


(v) { 2 }


(vi) { x : x is an odd prime number }

Question 8.


Which of the following pairs of sets are disjoint


(i) {1, 2, 3, 4}, and {x : x is a natural number and 4 ≤ x ≤ 6 }


(ii) { a, e, i, o, u }, and { c, d, e, f }


(iii) {x : x is an even integer }, and {x : x is an odd integer}

Answer 8.


(iii)

Question 9.


If


A = {3, 6, 9, 12, 15, 18, 21},


B = { 4, 8, 12, 16, 20 },


C = { 2, 4, 6, 8, 10, 12, 14, 16 },


D = {5, 10, 15, 20 };


find


(i) A − B


(ii) A − C


(iii) A − D


(iv) B − A


(v) C − A


(vi) D − A


(vii) B − C


(viii) B − D


(ix) C − B


(x) D − B


(xi) C − D


(xii) D − C

Answer 9.


(i) {3, 6, 9, 15, 18, 21}


(ii) {3, 9, 15, 18, 21 }


(iii) {3, 6, 9, 12, 18, 21}


(iv) {4, 8, 16, 20 )


(v) { 2, 4, 8, 10, 14, 16 }


(vi) { 5, 10, 20 }


(vii) { 20 }


(viii) { 4, 8, 12, 16 }


(ix) { 2, 6, 10, 14}


(x) { 5, 10, 15 }


(xi) {2, 4, 6, 8, 12, 14, 16}


(xii) {5, 15, 20}

Question 10.


If


X= { a, b, c, d }, and


Y = { f, b, d, g},


find


(i) X − Y


(ii) Y − X


(iii) X ∩ Y

Answer 10.


(i) { a, c }


(ii) {f, g }


(iii) { b , d }

Question 11.


If


R is the set of real numbers, and


Q is the set of rational numbers,


then what is R − Q?

Answer 11.


Set of irrational numbers

Question 12.


State whether each of the following statement is true or false. Justify your answer.


(i) { 2, 3, 4, 5 }, and { 3, 6} are disjoint sets.


(ii) { a, e, i, o, u }, and { a, b, c, d } are disjoint sets.


(iii) { 2, 6, 10, 14 }, and { 3, 7, 11, 15} are disjoint sets.


(iv) { 2, 6, 10 }, and { 3, 7, 11} are disjoint sets.

Answer 12.


(i) F


(ii) F


(iii) T


(iv) T