2.5 Miscellaneous Examples

Example 18

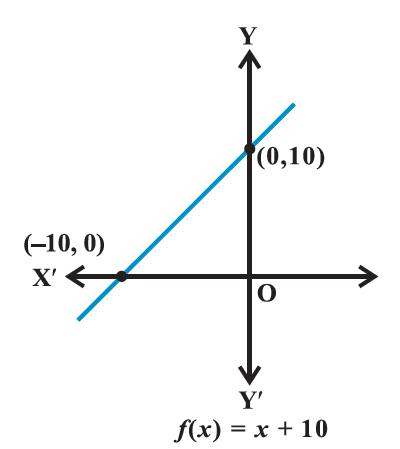
Let R be the set of real numbers. Define the real function f: R → R by f(x) = x + 10 and sketch the graph of this function.

Solution:

Here f(0) = 10, f(1) = 11, f(2) = 12, ..., f(10) = 20, etc., and f(−1) = 9, f(−2) = 8, ..., f(−10) = 0 and so on.

Therefore, shape of the graph of the given function assumes the form as shown in Figure 2.16.

Figure 2.16

Remark: The function f defined by f(x) = mx + c, x ∈ R, is called linear function, where m and c are constants. Above function is an example of a linear function.

Example 19

Let R be a relation from Q to Q defined by R = {(a, b) : a, b ∈ Q and a − b ∈ Z}. Show that


(i) (a, a) ∈ R for all a ∈ Q


(ii) (a, b) ∈ R implies that (b, a) ∈ R


(iii) (a, b) ∈ R and (b, c) ∈ R implies that (a, c) ∈ R

Solution:

(i) Since, a − a = 0 ∈ Z, if follows that (a, a) ∈ R.


(ii) (a, b) ∈ R implies that a − b ∈ Z. So, b − a ∈ Z. Therefore, (b, a) ∈ R


(iii) (a, b) and (b, c) ∈ R implies that a − b ∈ Z. b − c ∈ Z. So, a − c = (a − b) + (b − c) ∈ Z. Therefore, (a, c) ∈ R

Example 20

Let f = {(1, 1), (2, 3), (0, −1), (−1, −3)} be a linear function from Z into Z. Find f(x).

Solution:

Since f is a linear function, f (x) = mx + c. Also, since (1, 1), (0, − 1) ∈ R, f (1) = m + c = 1 and


f (0) = c = −1. This gives m = 2 and f(x) = 2x − 1.

Example 21

Find the domain of the function f(x) = (x^2 + 3x + 5)/(x^2 − 5x + 4)

Solution:

Since x^2 − 5x + 4 = (x − 4) (x −1), the function f is defined for all real numbers except at x = 4 and x = 1. Hence the domain of f is R − {1, 4}.

Example 22

The function f is defined by


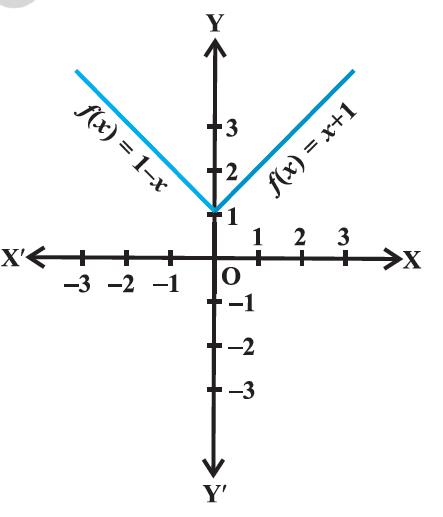
f (x) = {1, − x, x < 0; 1, x = 0; x + 1, x > 0


Draw the graph of f (x).

Solution:

Here, f(x) = 1 − x, x < 0, this gives


f(− 4) = 1 − (− 4) = 5;


f(− 3) =1 − (− 3) = 4,


f(− 2) = 1 − (− 2) = 3


f(−1) = 1 − (−1) = 2; etc,


and f(1) = 2,


f (2) = 3,


f (3) = 4


f(4) = 5 and so on for f(x) = x + 1, x > 0.

Thus, the graph of f is as shown in Figure 2.17

Figure 2.17