2.4 Functions

NCERT Class 11 books for blind and visually impaired students.

In this Section, we will study a special type of relation called 'function'. It is one of the most important concepts in mathematics. We can, visualise a function as a rule, which produces new elements out of some given elements. There are many terms such as ‘map’, or ‘mapping’, used to denote a function.

Definition 5

A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.

In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element.

If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.

The function f from A to B is denoted by f: A → B.

Looking at the previous examples, we can easily see that the relation in Example 7 is not a function because the element 6 has no image.

Again, the relation in Example 8 is not a function because the elements in the domain are connected to more than one image. Similarly, the relation in Example 9 is also not a function. (Why?) In the examples given below, we will see many more relations some of which are functions and some are not.

Example 10

Let N be the set of natural numbers and the relation R be defined on N such that


R = {(x, y) : y = 2x, x, y ∈ N}.


What is the domain, co-domain and range of R? Is this relation a function?

Solution:

The domain of R is the set of natural numbers N.


The codomain is also N. The range is the set of even natural numbers.

Since every natural number n has one and only one image, this relation is a function.

Example 11

Examine each of the following relations given below and state in each case, giving reasons whether it is a function or not?


(i) R = {(2, 1), (3, 1), (4, 2)},


(ii) R = {(2, 2), (2, 4), (3, 3), (4, 4)}


(iii) R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}

Solution:

(i) Since 2, 3, 4 are the elements of domain of R having their unique images, this relation R is a function.

(ii) Since the same first element 2 corresponds to two different images 2 and 4, this relation is not a function.

(iii) Since every element has one and only one image, this relation is a function.

Definition 6

A function which has either R or one of its subsets as its range is called a real valued function. Further, if its domain is also either R or a subset of R, it is called a real function.

Example 12

Let N be the set of natural numbers. Define a real valued function f : N → N by f (x) = 2x + 1. Using this definition, complete the table given below.

x	y
1	f(1) = . . .
2	f(2) = . . .
3	f(3) = . . .
4	f(4) = . . .
5	f(5) = . . .
6	f(6) = . . .
7	f(7) = . . .

Solution:

The completed table is given below:

X	y
1	f(1) = 3
2	f(2) = 5
3	f(3) = 7
4	f(4) = 9
5	f(5) = 11
6	f(6) = 13
7	f(7) = 15

2.4.1 Some functions and their graphs

(i) Identity function

Let R be the set of real numbers. Define the real valued function


f : R → R by y = f(x) = x, for each x ∈ R.


Such a function is called the identity function.


Here the domain and range of f are 'R'. The graph is a straight line as shown in Figure 2.8. It passes through the origin, and is inclined to the x-axis at 45°.

Figure 2.8

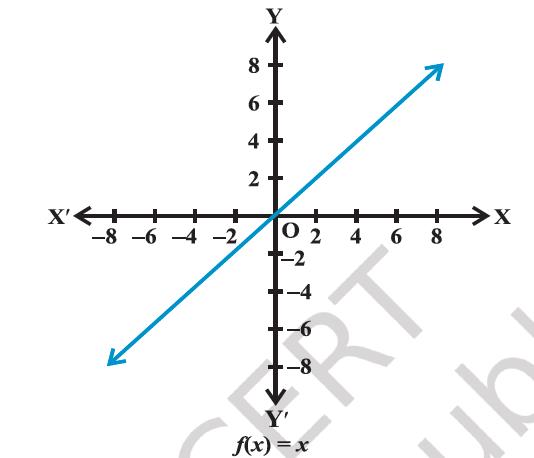
(ii) Constant function

Define the function f: R → R by y = f (x) = c, x ∈ R where c is a constant and each x ∈ R.


Here domain of f is R and its range is {c}.

Figure 2.9

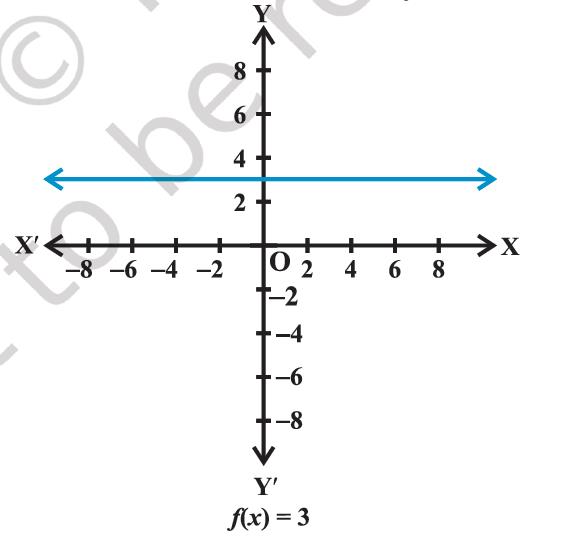
The graph is a line parallel to x-axis. For example, if f(x) = 3, for each x ∈ R, then its graph will be a line as shown in the Figure 2.9.

(iii) Polynomial function

A function f : R → R is said to be a polynomial function if for each x in R, y = f (x) = a_0 + a_1 x + a_2 x^2 + . . . + a_n x^n, where n is a non-negative integer and a_0, a_1, a_2, . . . , a_n ∈ R.

The functions defined by


f(x) = x^3 − x^2 + 2, and


g(x) = x^4 + √2 x


are some examples of polynomial functions, whereas the function


h defined by h(x) = x^(2/3) + 2x is not a polynomial function.(Why?)

Example 13

Define the function f: R → R by y = f(x) = x^2, x ∈ R. Complete the Table given below by using this definition. What is the domain and range of this function? Draw the graph of f.

x	y = f(x) = x^2
−4	-
−3	-
−2	-
−1	-
0	-
1	-
2	-
3	-
4	-

Solution:

The completed Table is given below:

x	y = f(x) = x^2
−4	16
−3	9
−2	4
−1	1
0	0
1	1
2	4
3	9
4	16

Domain of f = {x : x ∈ R}.


Range of f = {x^2 : x ∈ R}.


The graph of f is given by Figure 2.10

Figure 2.10

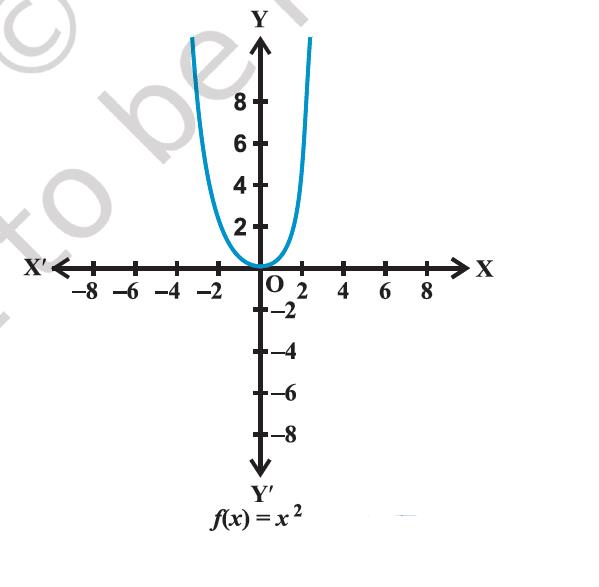
Example 14

Draw the graph of the function f : R → R defined by f (x) = x^3, x ∈ R.

Solution:

We have


f(0) = 0,


f(1) = 1,


f(−1) = −1,


f(2) = 8,


f(−2) = −8,


f(3) = 27,


f(−3) = −27, etc.

Therefore, f = {(x,x^3): x ∈ R}.

The graph of f is given in Figure 2.11.

Figure 2.11

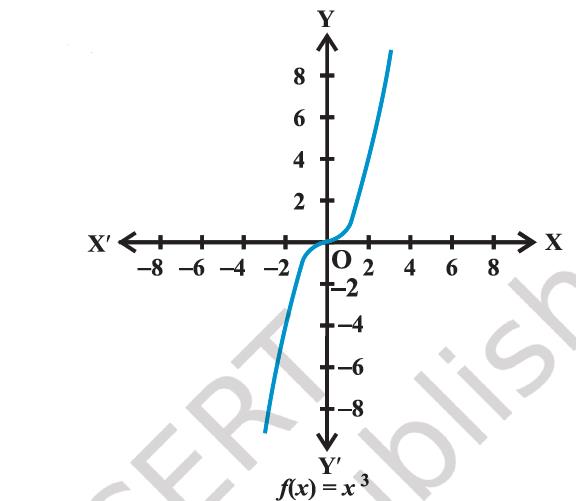
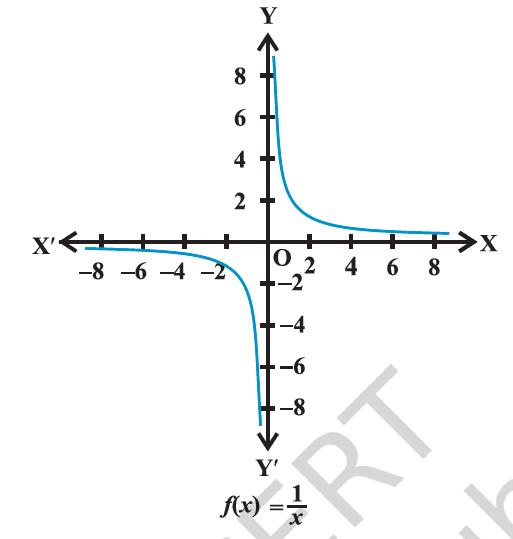
(iv) Rational functions

Rational functions are functions of the type f(x) / g(x), where f(x) and g(x) are polynomial functions of x defined in a domain, where g(x) ≠ 0.

Example 15

Define a real valued function f : R − {0} → R defined by f (x) = 1/x, x ∈ R − {0}. Complete the Table given below using this definition. What is the domain and range of this function?

x	y = 1/x
−2	. . .
−1.5	. . .
−1	. . .
−0.5	. . .
0.25	. . .
0.5	. . .
1	. . .
1.5	. . .
2	. . .

Solution:

The completed Table is given by

x	y = 1/x
−2	−0.5
−1.5	−0.67
−1	−1
−0.5	−2
0.25	4
0.5	2
1	1
1.5	0.67
2	0.5

The domain is all real numbers except 0 and its range is also all real numbers except 0. The graph of f is given in Figure 2.12.

Figure 2.12

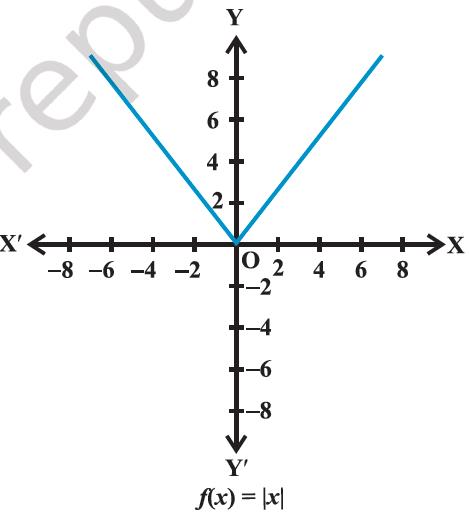
(v) The Modulus function

The function f: R → R defined by f(x) = |x| for each x ∈ R is called modulus function. For each non-negative value of x, f(x) is equal to x. But for negative values of x, the value of f(x) is the negative of the value of x, i.e.,


f(x) = {[x, x ≥ 0]; [−x, x < 0]

The graph of the modulus function is given in Figure 2.13.

Figure 2.13

(vi) Signum function

The function f: R → R defined by

f(x) = {(1, if x > 0); (0, if x = 0); (−1, if x < 0)

is called the signum function. The domain of the signum function is R and the range is the set {−1, 0, 1}. The graph of the signum function is given by the Figure 2.14.

Figure 2.14

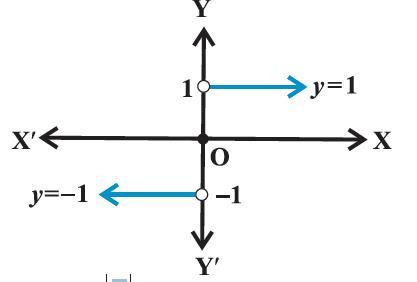
f(x) = |x|/x, x not 0 and 0 for x = 0

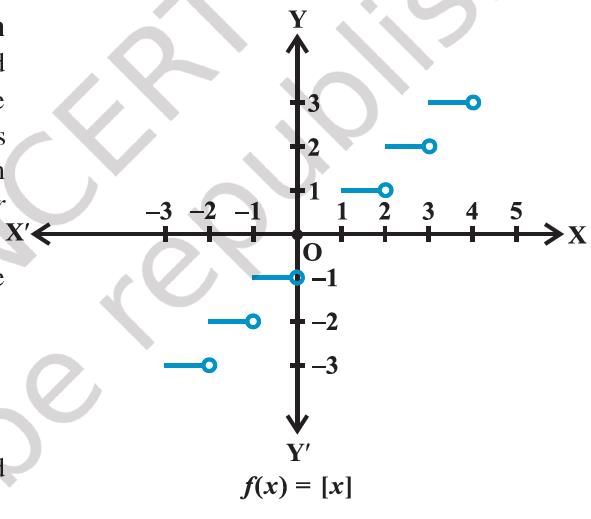
(vii) Greatest integer function

The function f: R → R defined by f(x) = [x], x ∈ R assumes the value of the greatest integer, less than or equal to x. Such a function is called the greatest integer function.

From the definition of [x], we can see that

[x] = −1 for −1 ≤ x < 0

[x] = 0 for 0 ≤ x < 1

[x] = 1 for 1 ≤ x < 2

[x] = 2 for 2 ≤ x < 3 and

so on.

The graph of the function is shown in Figure 2.15.

Figure 2.15

2.4.2 Algebra of real functions

In this Section, we shall learn how to add two real functions, subtract a real function from another, multiply a real function by a scalar (here by a scalar we mean a real number), multiply two real functions and divide one real function by another.

(i) Addition of two real functions

Let f : X → R and g : X → R be any two real functions, where X ⊂ R. Then, we define


(f+g) : X → R by (f + g) (x) = f (x) + g (x), for all x ∈ X.

(ii) Subtraction of a real function from another

Let f : X → R and g: X → R be any two real functions, where X ⊂ R. Then, we define


(f − g) : X → R by (f − g) (x) = f(x) − g(x), for all x ∈ X.

(iii) Multiplication by a scalar

Let f : X → R be a real valued function and α be a scalar. Here by scalar, we mean a real number. Then the product α f is a function from X to R defined by


(α f ) (x) = α f (x), x ∈ X.

(iv) Multiplication of two real functions

The product (or multiplication) of two real functions f: X → R and g: X → R is a function fg: X → R defined by


(fg) (x) = f(x) g(x), for all x ∈ X.

This is also called point wise multiplication.

(v) Quotient of two real functions

Let f and g be two real functions defined from X → R, where X ⊂ R. The quotient of f by g denoted by f/g is a function defined by,


(f/g)(x) = f(x)/g(x), provided g(x) ≠ 0, x ∈ X

Example 16

Let f(x) = x^2 and g(x) = 2x + 1 be two real functions. Find


(f + g) (x),


(f − g) (x),


(fg) (x),


(f/g) (x).

Solution:

We have,


(f + g) (x) = x^2 + 2x + 1,


(f − g) (x) = x^2 − 2x − 1,


(fg) (x) = x^2(2x + 1) = 2x^3 + x^2,


(f/g)(x) = x^2/(2x + 1), x ≠ −1/2

Example 17

Let f(x) = √x and g(x) = x be two functions defined over the set of nonnegative real numbers.


Find


(f + g) (x),


(f − g) (x),


(fg) (x) and


(f/g)(x).

Solution:

We have


(f + g) (x) = √x + x,


(f − g) (x) = √x − x ,


(fg) (x) = √x(x) = x^(3/2) and


(f/g)(x) = √x/x = x^−(1/2), x ≠ 0

EXERCISE 2.3

Question 1.


Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.


(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}


(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}


(iii) {(1,3), (1,5), (2,5)}.

Answer 1.


(i) yes, Domain = {2, 5, 8, 11, 14, 17}, Range = {1}


(ii) yes, Domain = (2, 4, 6, 8, 10, 12, 14}, Range = {1, 2, 3, 4, 5, 6, 7}


(iii) No.

Question 2.


Find the domain and range of the following real functions:


(i) f(x) = − |x|


(ii) f(x) = √(9 − x^2) .

Answer 2.


(i) Domain = R, Range = (−∞, 0]


(ii) Domain of function = {x : −3 ≤ x ≤ 3}


Range of function = {x : 0 ≤ x ≤ 3}

Question 3.


A function f is defined by f(x) = 2x − 5. Write down the values of


(i) f (0),


(ii) f (7),


(iii) f (−3).

Answer 3.


(i) f (0) = −5


(ii) f (7) = 9


(iii) f (−3) = −11

Question 4.


The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = (9C/5) + 32. Find


(i) t(0)


(ii) t(28)


(iii) t(−10)


(iv) The value of C, when t(C) = 212.

Answer 4.


(i) t (0) = 32


(ii) t (28) = 412/5


(iii) t (−10) = 14


(iv) 100

Question 5.


Find the range of each of the following functions.


(i) f (x) = 2 − 3x, x ∈ R, x > 0.


(ii) f (x) = x^2 + 2, x is a real number.


(iii) f (x) = x, x is a real number.

Answer 5.


(i) Range = ( − ∞, 2)


(ii) Range = [2, ∞)


(iii) Range = R