1.8 Venn Diagrams - Sets - Class 11 Mathematics

Submitted by superadmin on Mon, 21/04/2025 - 15:12

1.8 Venn Diagrams

NCERT Class 11 Mathematics for blind and visually impaired students made screen readable by Professor T K Bansal.

Most of the relationships between sets, can be represented by means of diagrams, which are known as Venn diagrams. Venn diagrams are named after the English logician, John Venn (1,834-1,883). These diagrams consist of rectangles and closed curves usually circles. The universal set is represented usually by a rectangle and its subsets by circles.

In a Venn diagram, the elements of the sets are written in their respective circles (Figures 1.2 and 1.3)

Figure 1.2

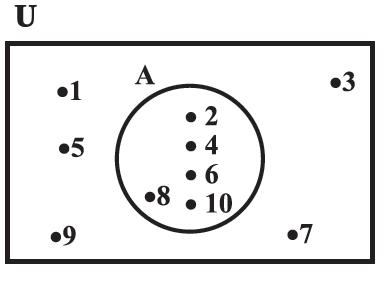
Shows a large rectangle, that is marked as U. Inside the rectangle, there is a circle that represents Set a. Points 2, 4, 6, 8, and 10 are marked inside the circle, whereas, Points 1, 3, 5, 7, and 9 are marked outside the circle. By Dr. T K Bansal

Illustration 1

In Figure 1.2, U = {1, 2, 3, ..., 10} is the universal set of which A = {2, 4, 6, 8, 10} is a subset of the universal set.

Figure 1.3

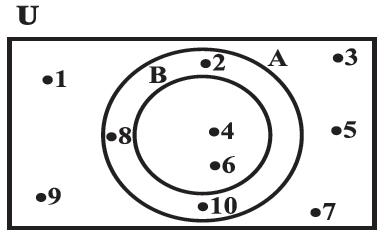
Shows the universal set U, that contains the same 10 points as in figure 1.2. Circles representing sets A and B are also shown. Points 2, 4, 6, 8, and 10 are marked inside A. Points 4, and 6 are marked inside B. Clearly, set B lies completely inside set a. By Dr T K Bansal

Illustration 2

In Figure 1.3, U = {1, 2, 3, ..., 10} is the universal set of which A = {2, 4, 6, 8, 10} and B = {4, 6} are subsets, and also B ⊂ A.

The reader will see an extensive use of the Venn diagrams when we will discuss the union, intersection and difference of sets.