1.3 Types of Functions

Screen Readable NCERT Class 12 Mathematics Textbook for Blind and Visually Impaired Students prepared by Dr t K Bansal.

The notion of a function along with some special functions like identity function, constant function, polynomial function, rational function, modulus function, signum function etc along with their graphs have been given in Class 11.

Addition, subtraction, multiplication and division of two functions have also been studied by you in your earlier class. As the concept of function is of paramount importance in mathematics and among other disciplines as well, we would like to extend our study about function from where we finished earlier. In this section, we would like to study different types of functions.

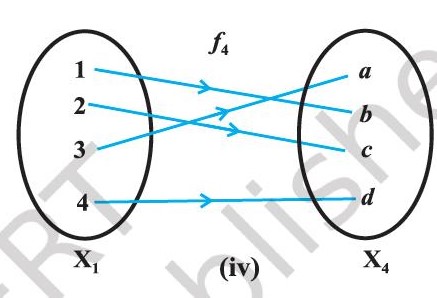
Consider the functions f_1, f_2, f_3 and f_4 (read as, f1, f2, f3 and f4), given by the following diagrams.

In Figure 1.2, we observe that the images of distinct elements of X1 under the function f1 are distinct, but the image of two distinct elements 1 and 2 of X1 under f2 is same, namely b. Further, there are some elements like e and f in X2 which are not images of any element of X1 under f1, while all elements of X3 are images of some elements of X1 under f3. The above observations lead to the following definitions:

Definition 5

A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct, i.e., for every x1, x2 ∈ X, f (x1) = f (x2) implies x1 = x2. Otherwise, f is called many-one function.

The function f1 and f4 in Figure 1.2 (i) and (iv) are one-one and the function f2 and f3 in Figure 1.2 (ii) and (iii) are many-one.

Definition 6

A function f : X → Y is said to be onto (or subjective), if every element of Y is the image of some element of X under f, i.e., for every y ∈ Y, there exists an element x in X such that f (x) = y.

The function f3 and f4 in Figure 1.2 (iii), (iv) are onto and the function f1 in Figure 1.2 (i) is not onto as elements e, f in X2 are not the image of any element in X1 under f1.

Figure 1.2(i)

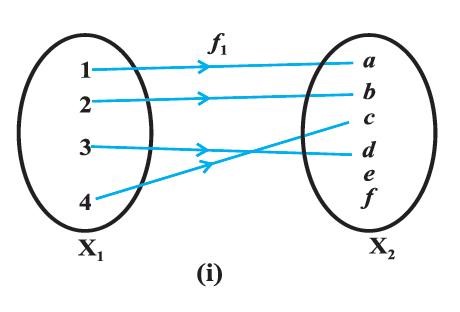
Figure 1.2(ii)

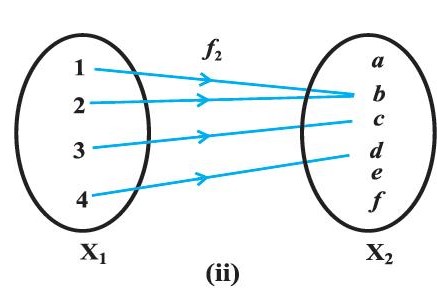
Figure 1.2(iii)

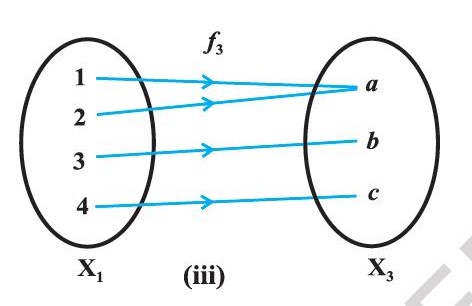
Figure 1.2 (iv)

Remark:


f : X → Y is onto if and only if Range of f = Y.

Definition 7

A function f : X → Y is said to be one-one and onto (or bijective), if f is both one-one and onto.

The function f4 in Fig 1.2 (iv) is one-one and onto.

Example 7

Let A be the set of all 50 students of Class 10 in a school. Let f : A → N be function defined by


f (x) = roll number of the student x.


Show that f is one-one but not onto.

Solution :

No two different students of the class can have the same rollnumber. Therefore, f must be one-one.


We can assume without any loss of generality that rollnumbers of students are from 1 to 50. This implies that 51 in N is not rollnumber of any student of the class, so that 51 cannot be image of any element of X under f. Hence, f is not onto.

Example 8

Show that the function f : N → N, given by


f (x) = 2x,


is one-one but not onto.

Solution :

The function f is one-one, for f (x1) = f (x2)


⇒ 2x1 = 2x2


⇒ x1 = x2.

Further, f is not onto, as for 1 ∈ N, there does not exist any x in N such that f (x) = 2x = 1.

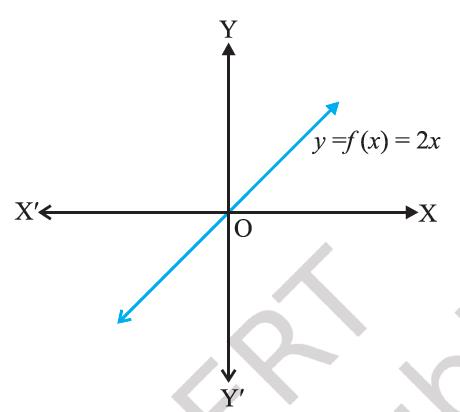
Example 9

Prove that the function f : R → R, given by


f (x) = 2x,


is one-one and onto.

Solution:

f is one-one, as f (x1) = f (x2)


⇒ 2x1 = 2x2


⇒ x1 = x2.

Also, given any real number y in R, there exists y/2 in R such that f (y/2) = 2 . (y/2) = y.

Hence, f is onto.

Figure 1.3

Example 10

Show that the function f : N → N, given by


f (1) = f (2) = 1 and f (x) = x − 1, for every x > 2,


is onto but not one-one.

Solution :

f is not one-one, as f (1) = f (2) = 1.


But f is onto, as given any y ∈ N, y ≠1, we can choose x as y + 1 such that f (y + 1) = y + 1 − 1 = y.

Also for 1 ∈ N, we have f (1) = 1.

Example 11

Show that the function f : R → R, defined as


f (x) = x^2,


is neither one-one nor onto.

Solution :

Figure 1.4

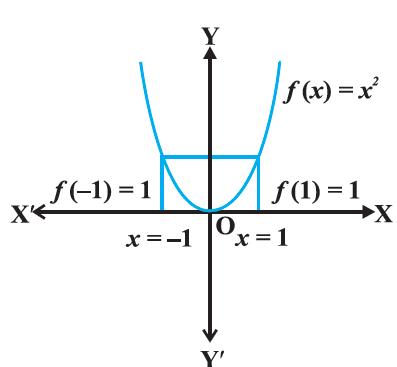
The image of 1 and −1 under d is 1.

Solution:

Since f (− 1) = 1 = f (1), f is not one-one.


Also, the element − 2 in the co-domain R is not image of any element x in the domain R (Why?). Therefore f is not onto.

Example 12

Show that f : N → N, given by


f(x) = x + 1, if x is odd; x − 1, if x is even is both one-one and onto.

Solution:

Suppose f (x1) = f (x2).


Note that if x1 is odd and x2 is even, then we will have


x1 + 1 = x2 − 1, i.e.,


x2 − x1 = 2 which is impossible.


Similarly, the possibility of x1 being even and x2 being odd can also be ruled out, using the similar argument. Therefore, both x1 and x2 must be either odd or even.


Suppose both x1 and x2 are odd. Then f (x1) = f (x2)


⇒ x1 + 1 = x2 + 1


⇒ x1 = x2.

Similarly, if both x1 and x2 are even, then also f (x1) = f (x2)


⇒ x1 − 1 = x2 − 1


⇒ x1 = x2.

Thus, f is one-one.

Also, any odd number 2r + 1 in the co-domain N is the image of 2r + 2 in the domain N and any even number 2r in the co-domain N is the image of 2r − 1 in the domain N. Thus, f is onto.

Example 13

Show that an onto function f : {1, 2, 3} → {1, 2, 3} is always one-one.

Solution :

Suppose f is not one-one. Then there exists two elements, say 1 and 2 in the domain whose image in the co-domain is same. Also, the image of 3 under f can be only one element. Therefore, the range set can have at the most two elements of the co-domain {1, 2, 3}, showing that f is not onto, a contradiction. Hence, f must be one-one.

Example 14

Show that a one-one function f : {1, 2, 3} → {1, 2, 3} must be onto.

Solution :

Since f is one-one, three elements of {1, 2, 3} must be taken to 3 different elements of the co-domain {1, 2, 3} under f. Hence, f has to be onto.

Remark:


The results mentioned in Examples 13 and 14 are also true for an arbitrary finite set X, i.e., a one-one function f : X → X is necessarily onto and an onto map f : X → X is necessarily one-one, for every finite set X.


In contrast to this, Examples 8 and 10 show that for an infinite set, this may not be true. In fact, this is a characteristic difference between a finite and an infinite set.

EXERCISE 1.2

Question 1


Show that the function f : R*→ R* defined by f (x) = 1/x is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true, if the domain R* is replaced by N with co-domain being same as R*?

Answer 1


No

Question 2


Check the injectivity and surjectivity of the following functions:


(i) f : N → N given by f (x) = x^2


(ii) f : Z → Z given by f (x) = x^2


(iii) f : R → R given by f (x) = x^2


(iv) f : N → N given by f (x) = x^3


(v) f : Z → Z given by f (x) = x^3

Answer 2


(i) Injective but not surjective


(ii) Neither injective nor surjective


(iii) Neither injective nor surjective


(iv) Injective but not surjective


(v) Injective but not surjective

Question 3


Prove that the Greatest Integer Function f : R → R, given by f (x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.

Question 4


Show that the Modulus Function f : R → R, given by f (x) = | x|, is neither one-one nor onto, where | x | is x, if x is positive or 0 and |x | is − x, if x is negative.

Question 5


Show that the Signum Function f : R → R, given by


f(x) = {1, if x > 0; 0, if x = 0; 1, if x < 0


is neither one-one nor onto.

Question 6


Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let


f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.

Question 7


In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.


(i) f : R → R defined by f (x) = 3 − 4x


(ii) f : R → R defined by f (x) = 1 + x^2

Answer 7


(i) One-one and onto


(ii) Neither one-one nor onto.

Question 8


Let A and B be sets. Show that f : A × B → B × A such that


f (a, b) = (b, a) is bijective function.

Question 9


Let f : N → N be defined by


f (n) = {n + 1/2, if n is odd; n/2, if n is even for all n ∈ N. State whether the function f is bijective. Justify your answer.

Answer 9


No

Question 10


Let A = R − {3} and B = R − {1}. Consider the function f : A → B defined by f(x) =


(x − 2/x − 3). Is f one-one and onto? Justify your answer.

Answer 10


Yes

Question 11


Let f : R → R be defined as f(x) = x^4. Choose the correct answer.


(A) f is one-one onto


(B) f is many-one onto


(C) f is one-one but not onto


(D) f is neither one-one nor onto.

Answer 11


D

Question 12


Let f : R → R be defined as f (x) = 3x. Choose the correct answer.


(A) f is one-one onto


(B) f is many-one onto


(C) f is one-one but not onto


(D) f is neither one-one nor onto.

Answer 12


A