1.2 Types of Relations

NCERT Class 12 Mathematics for blind and visually impaired students made screen readable by Professor T K Bansal.

In this section, we would like to study different types of relations. We know that a relation in a set A is a subset of A × A. Thus, the empty set φ and A × A are two extreme relations.

For illustration, consider a relation R in the set A = {1, 2, 3, 4} given by


R = {(a, b): a − b = 10}.


This is the empty set, as no pair (a, b) satisfies the condition a − b = 10.

Similarly, R′ = {(a, b) : | a − b | ≥ 0},


is the whole set A × A, as all pairs (a, b) in A × A satisfy | a − b | ≥ 0.

These two extreme examples lead us to the following definitions.

Definition 1

A relation R in a set A is called empty relation, if no element of A is related to any element of A, i.e., R = φ ⊂ A × A.

Definition 2

A relation R in a set A is called universal relation, if each element of A is related to every element of A, i.e., R = A × A.

Both the empty relation and the universal relation are sometimes called trivial relations.

Example 1

Let A be the set of all students of a boys school. Show that


the relation R in A given by R = {(a, b) : a is sister of b} is the empty relation


and, R′ = {(a, b) : the difference between heights of a and b is less than 3 meters} is the universal relation.

Solution :

Since the school is boys school, no student of the school can be a sister of any student of the school. Hence, R = φ, showing that R is the empty relation.

It is also obvious that the difference between heights of any two students of the school has to be less than 3 meters. This shows that R′ = A × A is the universal relation.

Remark:


In Class 11, we have seen two ways of representing a relation, namely raster method and set builder method. However, a relation R in the set {1, 2, 3, 4} defined by


R = {(a, b) : b = a + 1}


is also expressed as a R b if and only if b = a + 1, by many authors.


We may also use this notation, as and when convenient.

If (a, b) ∈ R, we say that a is related to b and we denote it as a R b.

One of the most important relation, which plays a significant role in Mathematics, is an equivalence relation.

To study equivalence relation, we first consider three types of relations, namely


reflexive,


symmetric and


transitive.

Definition 3

A relation R in a set A is called

(i) reflexive, if (a, a) ∈ R, for every a ∈ A,

(ii) symmetric, if (a1, a2) ∈ R implies that (a2, a1) ∈ R, for all a1, a2 ∈ A.

(iii) transitive, if (a1, a2) ∈ R and (a2, a3) ∈ R implies that (a1, a3) ∈ R, for all a1, a2, a3 ∈ A.

Definition 4

A relation R in a set A is said to be an equivalence relation if R is reflexive, symmetric and transitive.

Example 2

Let T be the set of all triangles in a plane with R a relation in T given by


R = {(T1, T2) : T1 is congruent to T2}.


Show that R is an equivalence relation.

Solution :

R is reflexive, since every triangle is congruent to itself.

Further, (T1, T2) ∈ R ⇒ T1 is congruent to T2 ⇒ T2 is congruent to T1 ⇒ (T2, T1) ∈ R. Hence, R is symmetric.

Moreover, (T1, T2), (T2, T3) ∈ R ⇒ T1 is congruent to T2 and T2 is congruent to T3 ⇒ T1 is congruent to T3 ⇒ (T1, T3) ∈ R. Hence, R is transitive.

Since R is Reflexive, Symmetric, and transitive, therefore, relation R is an equivalence relation.

Example 3

Let L be the set of all lines in a plane and R be the relation in L defined as


R = {(L1, L2) : L1 is perpendicular to L2}.


Show that R is symmetric but neither reflexive nor transitive.

Solution:

Figure 1.1

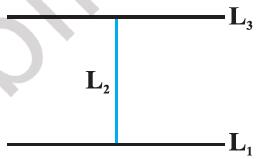
R is not reflexive, as a line L1 cannot be perpendicular to itself, i.e., (L1, L1) ∉ R.

R is symmetric


as (L1, L2) ∈ R


⇒ L1 is perpendicular to L2


⇒ L2 is perpendicular to L1


⇒ (L2, L1) ∈ R.

R is not transitive.


Indeed, if L1 is perpendicular to L2 and L2 is perpendicular to L3, then L1 can never be perpendicular to L3. In fact, L1 is parallel to L3, i.e.,


If (L1, L2) ∈ R, (L2, L3) ∈ R, then, (L1, L3) ∉ R.

Example 4

Show that the relation R in the set {1, 2, 3} given by


R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive.

Solution:

R is reflexive,


since (1, 1), (2, 2) and (3, 3) ∈ R.

Also, R is not symmetric,


as (1, 2) ∈ R but (2, 1) ∉ R.

Similarly, R is not transitive,


as (1, 2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R.

Example 5

Show that the relation R in the set Z of integers given by


R = {(a, b) : 2 divides (a − b)}


is an equivalence relation.

Solution:

R is reflexive, as 2 divides (a − a) ∀ a ∈ Z.

Further, if (a, b) ∈ R, then 2 divides a − b.


Therefore, 2 divides (b − a).


Hence, (b, a) ∈ R,


which shows that R is symmetric.

Similarly, if (a, b) ∈ R and (b, c) ∈ R,


then a − b and b − c are both divisible by 2.


Now, a − c = (a − b) + (b − c) is even (Why?).


So, (a − c) is divisible by 2.


This shows that R is transitive.

Thus, R is an equivalence relation in Z.

In Example 5, note that


all even integers are related to zero,


as (0, ± 2), (0, ± 4) etc., lie in R and


no odd integer is related to 0,


as (0, ± 1), (0, ± 3) etc., do not lie in R

Similarly, all odd integers are related to one and no even integer is related to one.


Therefore, the set E of all even integers and the set O of all odd integers are subsets of Z satisfying following conditions:

(i) All elements of E are related to each other and all elements of O are related to each other.


(ii) No element of E is related to any element of O and vice-versa.


(iii) E and O are disjoint and Z = E ∪ O.

The subset E is called the equivalence class containing zero and is denoted by [0].


Similarly, O is the equivalence class containing 1 and is denoted by [1].


Note that [0] ≠ [1],


[0] = [2r] and [1] = [2r + 1], r ∈ Z.

In fact, what we have seen above is true for an arbitrary equivalence relation R in a set X.


Given an arbitrary equivalence relation R in an arbitrary set X, R divides X into mutually disjoint subsets A i called partitions or subdivisions of X satisfying, where I is written as a subscript to capital A:

(i) all elements of A i are related to each other, for all I.


(ii) no element of A i is related to any element of A j ,


i ≠ j.


(iii) ∪ A j = X and A i ∩ A j = φ, i ≠ j.

The subsets A i are called equivalence classes.

The interesting part of the situation is that we can go reverse also.


For example,


consider a subdivision of the set Z given by three mutually disjoint subsets A1, A2 and A3 whose union is Z with

A1 = {x ∈ Z : x is a multiple of 3} = {..., − 6, − 3, 0, 3, 6, ...}


A2 = {x ∈ Z : x − 1 is a multiple of 3} = {..., − 5, − 2, 1, 4, 7, ...}


A3 = {x ∈ Z : x − 2 is a multiple of 3} = {..., − 4, − 1, 2, 5, 8, ...}

Define a relation R in Z given by R = {(a, b) : 3 divides (a – b)}. Following the arguments similar to those used in Example 5, we can show that R is an equivalence relation. Also, A1 coincides with the set of all integers in Z which are related to zero, A2 coincides with the set of all integers which are related to 1 and A3 coincides with the set of all integers in Z which are related to 2. Thus, A1 = [0], A2 = [1] and A3 = [2].


In fact, A1 = [3r], A2 = [3r + 1] and A3 = [3r + 2], for all r ∈ Z.

Example 6

Let R be the relation defined in the set A = {1, 2, 3, 4, 5, 6, 7} by


R = {(a, b) : both a and b are either odd or even}.


Show that R is an equivalence relation.


Further, show that all the elements of the subset {1, 3, 5, 7} are related to each other and


all the elements of the subset {2, 4, 6} are related to each other,


but no element of the subset {1, 3, 5, 7} is related to any element of the subset {2, 4, 6}.

Solution:

Given any element a in A, both a and a must be either odd or even, so that (a, a) ∈ R. Hence R is reflexive.


Further, (a, b) ∈ R ⇒ both a and b must be either odd or even ⇒ (b, a) ∈ R, i.e., R is symmetric.


Similarly, (a, b) ∈ R, and (b, c) ∈ R ⇒ all elements a, b, c, must be either even or odd simultaneously ⇒ (a, c) ∈ R. implies R is transitive.


Hence, R is an equivalence relation.

Further, all the elements of {1, 3, 5, 7} are related to each other, as all the elements of this subset are odd.


Similarly, all the elements of the subset {2, 4, 6} are related to each other, as all of them are even. Also, no element of the subset {1, 3, 5, 7} can be related to any element of {2, 4, 6}, as elements of {1, 3, 5, 7} are odd, while elements of {2, 4, 6} are even.

EXERCISE 1.1

Question 1


Determine whether each of the following relations are reflexive, symmetric and transitive:


(i) Relation R in the set A = {1, 2, 3, ..., 13, 14} defined as


R = {(x, y) : 3x − y = 0}


(ii) Relation R in the set N of natural numbers defined as


R = {(x, y) : y = x + 5 and x < 4}


(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as


R = {(x, y) : y is divisible by x}


(iv) Relation R in the set Z of all integers defined as


R = {(x, y) : x − y is an integer}


(v) Relation R in the set A of human beings in a town at a particular time given by


(a) R = {(x, y) : x and y work at the same place}


(b) R = {(x, y) : x and y live in the same locality}


(c) R = {(x, y) : x is exactly 7 cm taller than y}


(d) R = {(x, y) : x is wife of y}


(e) R = {(x, y) : x is father of y}

Answer 1


(i) Neither reflexive nor symmetric nor transitive.


(ii) Neither reflexive nor symmetric but transitive.


(iii) Reflexive and transitive but not symmetric.


(iv) Reflexive, symmetric and transitive.


(v) (a) Reflexive, symmetric and transitive.


(b) Reflexive, symmetric and transitive.


(c) Neither reflexive nor symmetric nor transitive.


(d) Neither reflexive nor symmetric but transitive.


(e) Neither reflexive nor symmetric nor transitive.

Question 2


Show that the relation R in the set R of real numbers, defined as


R = {(a, b) : a ≤ b^2} is neither reflexive nor symmetric nor transitive.

Question 3


Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as


R = {(a, b) : b = a + 1}


is reflexive, symmetric or transitive.

Answer 3


Neither reflexive nor symmetric nor transitive.

Question 4


Show that the relation R in R defined as


R = {(a, b) : a ≤ b},


is reflexive and transitive but not symmetric.

Question 5


Check whether the relation R in R defined by


R = {(a, b) : a ≤ b^3}


is reflexive, symmetric or transitive.

Answer 5


Neither reflexive nor symmetric nor transitive.

Question 6


Show that the relation R in the set {1, 2, 3} given by


R = {(1, 2), (2, 1)}


is symmetric but neither reflexive nor transitive.

Question 7


Show that the relation R in the set A of all the books in a library of a college, given by


R = {(x, y) : x and y have same number of pages}


is an equivalence relation.

Question 8


Show that the relation R in the set A = {1, 2, 3, 4, 5} given by


R = {(a, b) : |a − b| is even},


is an equivalence relation.


Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.

Question 9


Show that each of the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by


(i) R = {(a, b) : |a − b| is a multiple of 4}


(ii) R = {(a, b) : a = b}


is an equivalence relation. Find the set of all elements related to 1 in each case.

Answer 9


(i) {1, 5, 9},


(ii) {1}

Question 10


Give an example of a relation. Which is


(i) Symmetric but neither reflexive nor transitive.


(ii) Transitive but neither reflexive nor symmetric.


(iii) Reflexive and symmetric but not transitive.


(iv) Reflexive and transitive but not symmetric.


(v) Symmetric and transitive but not reflexive.

Question 11


Show that the relation R in the set A of points in a plane given by


R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin},


is an equivalence relation.


Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.

Question 12


Show that the relation R defined in the set A of all triangles as


R = {(T1, T2) : T1 is similar to T2},


is equivalence relation.


Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?

Answer 12


T1 is related to T3.

Question 13


Show that the relation R defined in the set A of all polygons as


R = {(P1, P2) : P1 and P2 have same number of sides},


is an equivalence relation.


What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?

Answer 13


The set of all triangles

Question 14


Let L be the set of all lines in X-Y plane and R be the relation in L defined as


R = {(L1, L2) : L1 is parallel to L2}.


Show that R is an equivalence relation.


Find the set of all lines related to the line y = 2x + 4.

Answer 14


The set of all lines y = 2x + c, c ∈ R

Question 15


Let R be the relation in the set {1, 2, 3, 4} given by


R = {(1, 2), (2, 2), (1, 1), (4, 4),


(1, 3), (3, 3), (3, 2)}.


Choose the correct answer.


(A) R is reflexive and symmetric but not transitive.


(B) R is reflexive and transitive but not symmetric.


(C) R is symmetric and transitive but not reflexive.


(D) R is an equivalence relation.

Answer 15


B

Question 16


Let R be the relation in the set N given by


R = {(a, b) : a = b − 2, b > 6}.


Choose the correct answer.


(A) (2, 4) ∈ R


(B) (3, 8) ∈ R


(C) (6, 8) ∈ R


(D) (8, 7) ∈ R

Answer 16


C