2.2 Cartesian Products of Sets

NCERT books for low vision students.

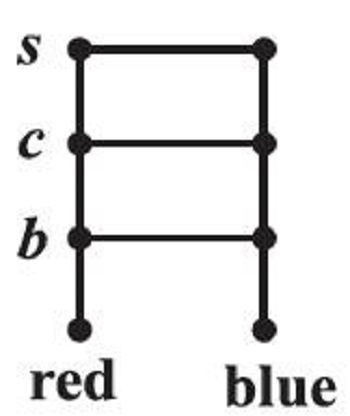
Suppose A is a set of 2 colours and B is a set of 3 objects, i.e.,


A = {red, blue} and B = {bag, coat, shirt},

How many pairs of coloured objects can be made from these two sets?

Proceeding in a very orderly manner, we can see that there will be 6 distinct pairs as given below:


(red, bag), (red, coat), (red, shirt), (blue, bag), (blue, coat), (blue, shirt).


Thus, we get 6 distinct objects (Figure 2.1).

Figure 2.1

Let us recall from our earlier classes that an ordered pair of elements taken from any two sets P and Q is a pair of elements written in round brackets and grouped together in a particular order, i.e., (p, q), where,p ∈ capital P and q ∈ capital Q . This leads to the following definition:

Definition 1

Given two non-empty sets P and Q. The Cartesian product P × Q is the set of all ordered pairs of elements from P and Q, i.e.,


P × Q = { (p,q) : p ∈ P, q ∈ Q }


If either P or Q is the null set, then P × Q will also be empty set,


i.e., P × Q = φ

From the illustration given above we note that


A × B = {(red,bag), (red,coat), (red,shirt), (blue,bag), (blue,coat), (blue,shirt)}.

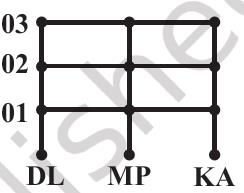
Again, consider the two sets:


A = {DL, MP, KA}, where DL, MP, KA represent Delhi, Madhya Pradesh, and Karnataka, respectively and


B = {01,02,03} representing codes for the licence plates of vehicles issued by DL, MP and KA .

If the three states, Delhi, Madhya Pradesh, and Karnataka were making codes for the licence plates of vehicles, with the restriction that the code begins with an element from set A, which are the pairs available from these sets and how many such pairs will there be (Figure 2.2)?

Figure 2.2

The available pairs are:


(DL,01), (DL,02), (DL,03),


(MP,01), (MP,02), (MP,03),


(KA,01), (KA,02), (KA,03)


and the product of set A and set B is given by


A × B =


{(DL,01), (DL,02), (DL,03),


(MP,01), (MP,02), (MP,03),


(KA,01), (KA,02), (KA,03)}.

It can easily be seen that there are 9 such pairs in the Cartesian product, since there are 3 elements in each of the two sets A and B. This gives us 9 possible codes. Also note that the order in which these elements are paired is crucial. For example, the code (DL, 01) will not be the same as the code (01, DL).

As a final illustration, consider the two sets A = {a1, a2} and B = {b1, b2, b3, b4} (Figure 2.3).

Figure 2.3

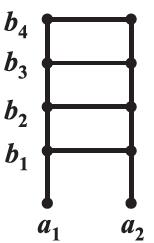
A × B


= {( a1, b1), (a1, b2), (a1, b3), (a1, b4),


(a2, b1), (a2, b2), (a2, b3), (a2, b4)}.

The 8 ordered pairs thus formed can represent the position of points in the plane if A and B are subsets of the set of real numbers and it is obvious that the point in the position (a1, b2) will be distinct from the point in the position (b2, a1).

Remarks:


(i) Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal.


(ii) If there are p elements in A and q elements in B, then there will be pq elements in A × B, i.e., if n(A) = p and n(B) = q, then n(A × B) = pq.


(iii) If A and B are non-empty sets and either A or B is an infinite set, then so is A × B.


(iv) A × A × A = {(a, b, c) : a, b, c ∈ A}.


Here (a, b, c) is called an ordered triplet.

Example 1

If (x + 1, y − 2) = (3,1), find the values of x and y.

Solution:

Since the ordered pairs are equal, the corresponding elements are equal.


Therefore x + 1 = 3 and y − 2 = 1.


Solving we get x = 2 and y = 3.

Example 2

If P = {a, b, c} and Q = {r}, form the sets P × Q and Q × P. Are these two products equal?

Solution:

By the definition of the Cartesian product, we get,


P × Q = {(a, r), (b, r), (c, r)} and


Q × P = {(r, a), (r, b), (r, c)}

Since, by the definition of equality of ordered pairs, the pair (a, r) is not equal to the pair (r, a), we conclude that P × Q ≠ Q × P.

However, the number of elements in each set is the same.

Example 3

Let A = {1,2,3}, B = {3,4}, and C = {4,5,6}. Find


(i) A × (B ∩ C)


(ii) (A × B) ∩ (A × C)


(iii) A × (B ∪ C)


(iv) (A × B) ∪ (A × C)

Solution:

(i) By the definition of the intersection of two sets, (B ∩ C) = {4}.


Therefore, A × (B ∩ C) = {(1,4), (2,4), (3,4)}.

(ii) Now (A × B) = {(1,3), (1,4), (2,3), (2,4), (3,3), (3,4)}


and (A × C) = {(1,4), (1,5), (1,6), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6)}


Therefore, (A × B) ∩ (A × C)


= {(1, 4), (2, 4), (3, 4)}.

(iii) Since, (B ∪ C) = {3, 4, 5, 6}, we have


A × (B ∪ C)


= {(1,3), (1,4), (1,5), (1,6),


(2,3), (2,4), (2,5), (2,6),


(3,3), (3,4), (3,5), (3,6)}.

(iv) Using the sets A × B and A × C from part (ii) above, we obtain


(A × B) ∪ (A × C)


= {(1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,3), (3,4), (3,5), (3,6)}.

Example 4

If P = {1, 2},


form the set P × P × P.

Solution:

We have, P × P × P = {(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2)}.

Example 5

If R is the set of all real numbers, what do the Cartesian products R × R and R × R × R represent?

Solution:

The Cartesian product R × R represents the set R × R = {(x, y) : x, y ∈ R} which represents the coordinates of all the points in two dimensional space and


the Cartesian product R × R × R represents the set R × R × R = {(x, y, z) : x, y, z ∈ R} which represents the coordinates of all the points in a three-dimensional space.

Example 6

If A × B = {(p, q), (p, r), (m, q), (m, r)},


find A and B.

Solution:

A = set of first elements = {p, m}


B = set of second elements = {q, r}.

EXERCISE 2.1

Question 1.


If (x/3 + 1, y − 2/3) = (5/3, 1/3), find the values of x and y.

Answer 1.


x = 2 and y = 1

Question 2.


If the set A has 3 elements and the set B = {3, 4, 5},


then find the number of elements in (A × B).

Answer 2.


The number of elements in A × B is 9.

Question 3.


If G = {7, 8} and H = {5, 4, 2},


find G × H and H × G.

Answer 3.


G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}


H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}

Question 4.


State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.


(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n), (n, m)}.


(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that


x ∈ A and y ∈ B.


(iii) If A = {1, 2}, B = {3, 4},


then A × (B ∩ φ) = φ.

Answer 4.


(i) False


P × Q = {(m, n), (m, m), (n, n), (n, m)}


(ii) True


(iii) True

Question 5.


If A = {−1, 1},


find A × A × A.

Answer 5.


A × A = {(− 1, − 1), (− 1, 1), (1, − 1), (1, 1)}


A × A × A = {(−1, −1, −1), (−1, −1, 1), (−1, 1, −1), (−1, 1, 1), (1, −1, −1), (1, −1, 1), (1, 1, −1), (1, 1, 1)}

Question 6.


If A × B = {(a, x), (a , y), (b, x), (b, y)}.


Find A and B.

Answer 6.


A = {a, b}, B = {x, y}

Question 7.


Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}.


Verify that


(i) A × (B ∩ C) = (A × B) ∩ (A × C).


(ii) A × C is a subset of B × D.

Question 8.


Let A = {1, 2} and B = {3, 4}.


Write A × B. How many subsets will A × B have? List them.

Answer 8.


A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}


A × B will have 2^4 = 16 subsets.

Question 9.


Let A and B be two sets such that n(A) = 3 and n(B) = 2.


If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

Answer 9.


A = {x, y, z} and B = {1, 2}

Question 10.


The Cartesian product A × A has 9 elements among which are found (−1, 0) and (0, 1). Find the set A and the remaining elements of A × A.

Answer 10.


A = {−1, 0, 1}, remaining elements of A × A are (−1, −1), (−1, 1), (0, ), (0, 0), (1, −1), (1, 0), (1, 1)