1.14 Supplementary reading for JEE Main and Advance

NCERT Class 11 Mathematics Textbook for blind and visually impaired students made screen readable by Professor T K Bansal.'

Please note: This content is taken from the previous edition of the NCERT Mathematics Textbook.

1.14.1 Power Set

Consider the set {1, 2}.


Let us write down all the possible subsets of the set {1, 2}.


We know that φ is a subset of every set . So, φ is a subset of {1, 2}.


We see that {1} and { 2 }are also subsets of {1, 2}.


Also, we know that every set is a subset of itself. So, { 1, 2 } is a subset of {1, 2}.


Thus, the set { 1, 2 } has, in all, four subsets, viz. φ, { 1 }, { 2 } and { 1, 2 }.


The set of all these subsets is called the power set of { 1, 2 }.

Definition

'The collection of all subsets of a set A is called the power set of A. It is denoted by P(A). In P(A), every element is a set itself.'

Thus, as in above, if A = { 1, 2 }, then


P(A) = { φ, {1}, {2}, {1, 2}}


Also, note that n[P(A)] = 4 = 2^2

In general, if A is a set with n(A) = m, then it can be shown that n[P(A)] = 2^m.

Question:


How many elements has P(A), if A = φ?

Answer:


1

---

1.14.2 Practical Problems on Union and Intersection of Two Sets

In earlier Section, we have learnt union, intersection and difference of two sets. In this Section, we will go through some practical problems related to our daily life. The formulae derived in this Section will also be used in subsequent Chapter on Probability (Chapter 16).

Let A and B be finite sets. If A ∩ B = φ, then


(i) n ( A ∪ B ) = n ( A ) + n ( B ) ... (1)

The elements in A ∪ B are either in A or in B but not in both as A ∩ B = φ. So, (1) follows immediately.

In general, if A and B are finite sets, then


(ii) n ( A ∪ B ) = n ( A ) + n ( B ) − n ( A ∩ B ) ... (2)

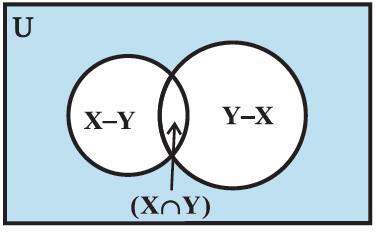
Note that the sets A − B, A ∩ B and B − A are disjoint and their union is A ∪ B (Figure 1.11).

Figure 1.11

Therefore


n ( A ∪ B) = n ( A − B) + n ( A ∩ B ) + n ( B − A )


= n ( A − B) + n ( A ∩ B ) + n ( B − A ) + n ( A ∩ B ) − n ( A ∩ B)


= n ( A ) + n ( B ) − n ( A ∩ B), which verifies (2)

(iii) If A, B and C are finite sets, then


n (A ∪ B ∪ C) = n (A) + n (B) + n (C) − n (A ∩ B) − n ( B ∩ C) − n ( A ∩ C ) + n ( A ∩ B ∩ C ) ... (3)

In fact, we have


n ( A ∪ B ∪ C ) = n (A) + n ( B ∪ C ) − n [ A ∩ ( B ∪ C ) ] [ by (2) ]


= n (A) + n ( B ) + n ( C ) − n ( B ∩ C ) − n [ A ∩ ( B ∪ C ) ] [ by (2) ]

Since A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ), we get


n [ A ∩ ( B ∪ C ) ] = n ( A ∩ B ) + n ( A ∩ C ) − n [ ( A ∩ B ) ∩ (A ∩ C)]


= n ( A ∩ B ) + n ( A ∩ C ) − n (A ∩ B ∩ C)

Therefore


n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) − n ( A ∩ B ) − n ( B ∩ C) − n ( A ∩ C ) + n ( A ∩ B ∩ C )

This proves (3).

Example 26

If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ∩ Y have ?

Solution:

Given that


n ( X ∪ Y ) = 50, n ( X ) = 28, n ( Y ) = 32, n (X ∩ Y) = ?

By using the formula


n ( X ∪ Y ) = n ( X ) + n ( Y ) − n ( X ∩ Y ),

we find that


n ( X ∩ Y ) = n ( X ) + n ( Y ) − n ( X ∪ Y )


= 28 + 32 − 50 = 10

Alternatively,

suppose n ( X ∩ Y ) = k, then


n ( X − Y ) = 28 − k ,


n ( Y − X ) = 32 − k


(by Venn diagram in Figure 1.12 )

Figure 1.12

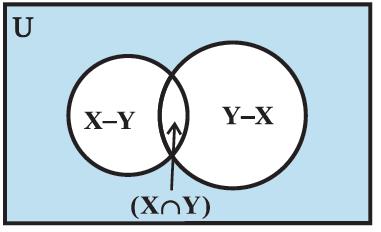
This gives 50 = n ( X ∪ Y ) = n (X − Y) + n (X ∩ Y) + n ( Y − X)


= ( 28 − k ) + k + (32 − k )


Hence k = 10.

Example 27

In a school there are 20 teachers who teach mathematics or physics. Of these, 12 teach mathematics and 4 teach both physics and mathematics. How many teach physics ?

Solution:

Let M denote the set of teachers who teach mathematics and P denote the set of teachers who teach physics. In the statement of the problem, the word ‘or’ gives us a clue of union and the word ‘and’ gives us a clue of intersection. We, therefore, have


n ( M ∪ P ) = 20 ,


n ( M ) = 12 and


n ( M ∩ P ) = 4


We wish to determine n ( P ).


Using the result


n ( M ∪ P ) = n ( M ) + n ( P ) − n ( M ∩ P ),


we obtain


20 = 12 + n ( P ) − 4


Thus n ( P ) = 12

Hence 12 teachers teach physics.

Example 28

In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football ?

Solution:

Let X be the set of students who like to play cricket and Y be the set of students who like to play football. Then X ∪ Y is the set of students who like to play at least one game, and X ∩ Y is the set of students who like to play both games.


Given


n ( X) = 24,


n ( Y ) = 16,


n ( X ∪ Y ) = 35,


n (X ∩ Y) = ?


Using the formula


n ( X ∪ Y ) = n ( X ) + n ( Y ) − n ( X ∩ Y ), we get


35 = 24 + 16 − n (X ∩ Y)


Thus, n (X ∩ Y) = 5


i.e., 5 students like to play both games.

Example 29

In a survey of 400 students in a school, 100 were listed as taking apple juice, 150 as taking orange juice, and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice nor orange juice.

Solution:

Let U denote the set of surveyed students and A denote the set of students taking apple juice and B denote the set of students taking orange juice. Then


n (U) = 400,


n (A) = 100,


n (B) = 150 and


n (A ∩ B) = 75.


Now n (A′ ∩ B′) = n (A ∪ B)′


= n (U) − n (A ∪ B)


= n (U) − n (A) − n (B) + n (A ∩ B)


= 400 − 100 − 150 + 75 = 225


Hence 225 students were taking neither apple juice nor orange juice.

Example 30

There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C1, 50 to chemical C2, and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to


(i) Chemical C1 but not chemical C2


(ii) Chemical C2 but not chemical C1


(iii) Chemical C1 or chemical C2

Solution:

Let, U denotes the universal set consisting of individuals suffering from the skin disorder, A denotes the set of individuals exposed to the chemical C1 and B denotes the set of individuals exposed to the chemical C2.

Here

Here,


n ( U) = 200,


n ( A ) = 120,


n ( B ) = 50 and


n ( A ∩ B ) = 30

Figure 1.13

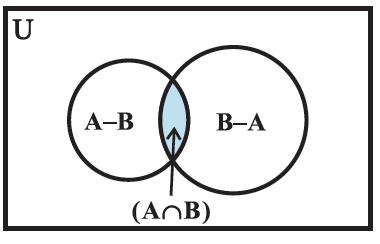
(i) From the Venn diagram given in Figure 1.13, we have

A = ( A − B ) ∪ ( A ∩ B ).


n (A) = n( A − B ) + n( A ∩ B ) (Since A − B) and A ∩ B are disjoint.)


or


n ( A − B ) = n ( A ) − n ( A ∩ B ) = 120 −30 = 90


Hence, the number of individuals exposed to


chemical C1 but not to chemical C2 is 90.

(ii) From the Figure 1.13,


we have


B = ( B − A) ∪ ( A ∩ B).


and so,


n (B) = n (B − A) + n ( A ∩ B)

>(Since B − A and A ∩ B are disjoint.)


or n ( B − A ) = n ( B ) − n ( A ∩ B )


= 50 − 30 = 20


Thus, the number of individuals exposed to chemical C2 and not to chemical C1 is 20.

(iii) The number of individuals exposed either to chemical C1 or to chemical C2, i.e.,


n ( A ∪ B ) = n ( A ) + n ( B ) − n ( A ∩ B )


= 120 + 50 − 30 = 140.

Example 31

For any sets A and B, show that P ( A ∩ B ) = P ( A ) ∩ P ( B ).

Solution

Let X ∈ P ( A ∩ B ).


Then X ⊂ A ∩ B. So, X ⊂ A and X ⊂ B.


Therefore, X ∈ P ( A ) and X ∈ P ( B ) which implies X ∈ P ( A ) ∩ P ( B).


This gives P ( A ∩ B ) ⊂ P ( A ) ∩ P ( B ).


Let Y ∈ P ( A ) ∩ P ( B ).


Then Y ∈ P ( A) and Y ∈ P ( B ).


So, Y ⊂ A and Y ⊂ B.


Therefore, Y ⊂ A Ç B, which implies Y ∈ P ( A ∩ B ).


This gives P ( A ) ∩ P ( B ) ⊂ P ( A ∩ B)


Hence P ( A ∩ B ) = P ( A ) ∩ P ( B ).

Example 32

A market research group conducted a survey of 1000 consumers and reported that 720 consumers like product A and 450 consumers like product B, what is the least number that must have liked both products?

Solution

Let U be the set of consumers questioned, S be the set of consumers who liked the product A and T be the set of consumers who like the product B. Given that


n ( U ) = 1000, n ( S ) = 720, n ( T ) = 450


So n ( S ∪ T ) = n ( S ) + n ( T ) − n ( S ∩ T )


= 720 + 450 − n (S ∩ T) = 1170 − n ( S ∩ T )


Therefore, n ( S ∪ T ) is maximum when n ( S ∩ T ) is least.


But S ∪ T ⊂ U implies n ( S ∪ T ) ≤ n ( U ) = 1000. So, maximum values of n ( S ∪ T ) is 1000.


Thus, the least value of n ( S ∩ T ) is 170.


Hence, the least number of consumers who liked both products is 170.

Example 33

Out of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct?

Solution

Let U be the set of car owners investigated, M be the set of persons who owned car A and S be the set of persons who owned car B.


Given that n ( U ) = 500, n (M ) = 400, n ( S ) = 200 and n ( S ∩ M ) = 50.


Then n ( S ∪ M ) = n ( S ) + n ( M ) − n ( S ∩ M ) = 200 + 400 − 50 = 550


But S ∪ M ⊂ U implies n ( S ∪ M ) ≤ n ( U ).


This is a contradiction. So, the given data is incorrect.

Example 34

A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 58 men and only three men got medals in all the three sports, how many received medals in exactly two of the three sports ?

Solution:

Let F, B and C denote the set of men who received medals in football, basketball and cricket, respectively.


Then n ( F ) = 38, n ( B ) = 15, n ( C ) = 20


n (F ∪ B ∪ C ) = 58 and n (F ∩ B ∩ C ) = 3


Therefore, n (F ∪ B ∪ C ) = n ( F ) + n ( B ) + n ( C ) − n (F ∩ B ) − n (F ∩ C ) − n (B ∩ C ) + n ( F ∩ B ∩ C ),


gives n ( F ∩ B ) + n ( F ∩ C ) + n ( B ∩ C ) = 18

Consider the Venn diagram as given in Figure 1.14

Figure 1.14

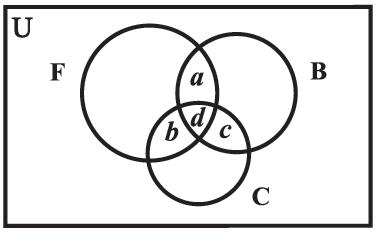
Here, a denotes the number of men who got medals in football and basketball only, b denotes the number of men who got medals in football and cricket only, c denotes the number of men who got medals in basket ball and cricket only and d denotes the number of men who got medal in all the three.

Thus, d = n ( F ∩ B ∩ C ) = 3 and a + d + b + d + c + d = 18


Therefore a + b + c = 9,


which is the number of people who got medals in exactly two of the three sports.

---

EXERCISE 1.6

Question 1.


If X and Y are two sets such that n ( X ) = 17, n ( Y ) = 23 and n ( X ∪ Y ) = 38, find n ( X ∩ Y ).

Answer 1.


2

Question 2.


If X and Y are two sets such that X ∪ Y has 18 elements, X has 8 elements and Y has 15 elements ; how many elements does X ∩ Y have?

Answer 2.


5

Question 3.


In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?

Answer 3.


50

Question 4.


If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩ T has 11 elements, how many elements does S ∪ T have?

Answer 4.


42

Question 5.


If X and Y are two sets such that X has 40 elements, X ∪ Y has 60 elements, and X ∩ Y has 10 elements, how many elements does Y have?

Answer 5.


30

Question 6.


In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?

Answer 6.


19

Question 7.


In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?

Answer 7.


25, 35

Question 8.


In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?

Answer 8.


60

Question 9.


Assume that P ( A ) = P ( B ). Show that A = B

Question 10.


Is it true that for any sets A and B, P ( A ) ∪ P ( B ) = P ( A ∪ B )? Justify your answer.

Answer 10.


False

Question 11.


In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee?

Answer 11.


325

Question 12.


In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?

Answer 12.


125

Question 13.


In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:


(i) the number of people who read at least one of the newspapers.


(ii) the number of people who read exactly one newspaper.

Answer 13.


(i) 52,


(ii) 30

Question 14.


In a survey it was found that 21 people liked product A, 26 liked products B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.

Answer 14.


11